 Our research focuses on finite element methods, domain decomposition methods, fast frequency sweep techniques, reduced order methods, reduced basis approximations, and their applications to the design of antennas and passive microwave circuits.
Our research focuses on finite element methods, domain decomposition methods, fast frequency sweep techniques, reduced order methods, reduced basis approximations, and their applications to the design of antennas and passive microwave circuits.
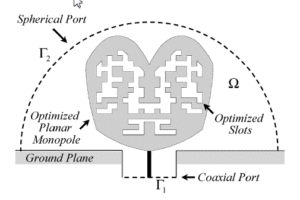
Most modern technology can not be conceived without appropriately handling electromagnetic phenomena. The rapid development of computing resources carried out throughout last century has made it possible to accurately simulate electromagnetic phenomena by means of numerically-rigorous full-wave methods. As a result, computational electromagnetics arises as a new research area for proper analysis, design and application of numerical methods to provide rigorous electromagnetic simulations. This reduces the need for expensive and time-consuming experimental testing and makes it possible to compare many different alternatives for design and optimization.
Computational electromagnetics is rapidly evolving with a great amount of challenging issues such as improving the capabilities to analyze every single electromagnetic phenomenon, the proper choice of spatial discretizations (finite differences, finite elements, finite volumes, boundary elements), and fast solvers for the discretized equations (multilevel techniques, domain decomposition methods, multipole, clustering and reduced-order models).
Current industry interests challenge traditional design to become full-wave optimization techniques demanding computer-aided design, where rapid evaluations in the parameter space are needed. As a result, all numerical schemes must be robust and reliable, otherwise we may not trust on these techniques for design automation and this would set them aside for academic purposes but never for industrial use.